Total Tayangan Halaman

Minggu, 30 Juni 2013

TAUTOLOGI DAN KONTRADIKSI, ALJABAR LOGIKA, NEGASI INGKAN

TAUTOLOGI DAN KONTRADIKSI, ALJABAR LOGIKA, NEGASI INGKAN
Tautologi adalah suatu proporsi majemuk yang selalu bernilai benar untuk semua kemungkinan kombinasi nilai kebenaran dari proporsi-proporsi pembentuknya

Contoh pada table kebenaran
p
\simp
p \vee \simp
B
S
S
B
B
B


Definisi :
Kontradiksi adalah suatu proporsi majemuk yang selalu bernilai salah untuk semua kemungkinan kombinasi nilai kebenaran dari proporsi-proporsi pembentuknya.

Contoh pada table kebenaran
p
\simp
p \wedge \simp
B
S
S
B
S
S
ALJABAR LOGIKA :
3.1    Pernyataan / Proposisi Pernyataan adalah suatu kalimat yang mempunyai nilai kebenaran (benar atau salah), tetapi tidak keduanya. Contoh 1 : p = Tadi malam BBM mulai naik (memiliki nilai kebenaran benar/true) q = 23 = 32 (memiliki nilai kebenaran salah/false) Contoh 2 : Berikut ini adalah beberapa contoh proposisi : a.    1 + 2 = 3 b.    Presiden RI tahun 2005 adalah SBY c.    6 adalah bilangan prima d.    Warna bendera RI adalah biru dan merah Kalimat-kalimat di atas adalah kalimat proposisi karena dapat diketahui benar/salahnya. Kalimat (a) dan (b) bernilai benar, sedangkan kalimat (c) dan (d) bernilai salah. Contoh 3 : Berikut ini adalah beberapa contoh kalimat yang bukan merupakan proposisi : a.    Di manakah letak pulau seribu? b.    Ersa lebih tua dari Arsi c.    x + y = 5 d.    2 mencintai 3 Kalimat (a) jelas bukan proposisi karena merupakan kalimat tanya sehingga tidak dapat ditentukan nilai kebenarannya. Kalimat (b) juga bukan proposisi karena ada banyak orang dibumi ini yang bernama Ersa dan Arsi. Kalimat tersebut tidak memberikan keterangan yang lebih spesifik sehingga tidak diketahui kebenaran bahwa Ersa lebih tua dari Arsi. Dalam kalimat (c), nilai kebenaran kalimat tergantung pada harga x dan y yang ada. Jika x =1 dan y = 4, maka kalimat tersebut menjadi kalimat yang benar. Tetapi jika x = 4 dan y = 5, maka kalimat tersebut menjadi kalimat yang salah. Jadi secara umum tidak dapat ditentukan apakah kalimat tersebut benar atau salah.     Kalimat (e), walaupun mempunyai susunan kalimat yang benar, tetapi tidak mempunyai arti karena relasi mencintai tidak berlaku pada bilangan. Oleh karena itu, kalimat tersebut tidak ditentukan benar atau salahnya.     Suatu pernyataan yang selalu benar dalam semua keadaan dinamakan tautologi , sedangkan pernyataan yang selalu salah dalam semua keadaan dinamakan kontradiksi.
3.2    Negasi / Ingkaran Negasi suatu kalimat akan mempunyai niali kebenaran yang berlawanan dengan nilai kebenaran kalimat aslinya. Jadi jika nilai p bernilai benar maka   bernilai salah. Sebaliknya jika p bernilai salah, maka   akan bernilai benar.
Diposting oleh di Tidak ada komentar:

DOMAIN, KODOMAIN DAN RANGE

Domain, Kodomain, dan Range
a. Domain adalah daerah kawan
b. Kodomain adalah daerah kawan
c. Range adalah daerah hasil dari himpunan bagian  dari kodomain.
Contoh
Himpunan A = {1,2,3,4,5,6,7} adalah domain
Himpunan B = {1,2,3,4,5,6,7,8} disebut kodomain
Himpunan semua peta = {2,3,4,5,6,7} disebut range
Tulisan ini disusun berdasarkan pembelajaran Matematika SMP Preceptorial.

Diposting oleh di Tidak ada komentar:

Rabu, 19 Juni 2013

RELASI


Contoh . Misalkan A = {1, 2, 3, 4}, dan relasi R di bawah ini didefinisikan pada himpunan A, maka
(a)      R = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3) } bersifat menghantar. Lihat tabel berikut:





Pengertian
Relasi adalah hubungan antara elemen himpunan dengan elemen himpunan yang lain. Cara
paling mudah untuk menyatakan hubungan antara elemen 2 himpunan adalah dengan
himpunan pasangan terurut. Himpunan pasangan terurut diperoleh dari perkalian
kartesian.

Definisi yang lain:
1. Perkalian kartesian (Cartesian products) antara himpunan A dan B ditulis: A x B
didefinisikan sebagai semua himpunan pasangan terurut dengan komponen pertama
adalah anggota himpunan A dan komponen kedua adlah anggota himpunan B.
A x B = { (x,y) / xÃŽA dan yÃŽB}

2. Relasi biner R antara A dan B adalah himpunan bagian dari A x B.
A disebut daerah asal dari R (domain) dan B disebut daerah hasil (range) dari R.

3.Relasi pada A adalah relasi dari A ke A.

contohnya :
  1. Misal X = {a,b,c}, B = {1,2}, maka : A x B = {(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)}
  2. Misal R adalah relasi pada A = {2,3,4,8,9} yang didefinisikan oleh (x,y)ÃŽR jika x
    adalah factor prima dari y, maka:
    R = {(2,2), (2,4), (2,8), (3,3), (3,9)}
Representasi Relasi
1. Representasi Relasi dengan Diagram Panah
 
 2. Representasi Relasi dengan Tabel
•    Kolom pertama tabel menyatakan daerah asal, sedangkan kolom kedua menyatakan daerah hasil.

3. Representasi Relasi dengan Matriks
•    Misalkan R adalah relasi dari A = {a1, a2, …, am} dan B = {b1, b2, …, bn}.
•    Relasi R dapat disajikan dengan matriks M = [mij],
        
yang dalam hal ini:

 Contoh . Relasi R pada Contoh 3 dapat dinyatakan dengan matriks








dalam hal ini, a1 = Amir, a2 = Budi, a3 = Cecep, dan b1 = IF221,
b2 = IF251, b3 = IF342, dan b4 = IF323.

Relasi R pada Contoh 4 dapat dinyatakan dengan matriks





yang dalam hal ini, a1 = 2, a2 = 3, a3 = 4, dan b1 = 2, b2 = 4, b3 = 8, b4 = 9, b5 = 15.

4.  Representasi Relasi dengan Graf Berarah
•    Relasi pada sebuah himpunan dapat direpresentasikan secara grafis dengan graf berarah (directed graph atau digraph)
•    Graf berarah tidak didefinisikan untuk merepresentasikan relasi dari suatu himpunan ke himpunan lain.
•    Tiap elemen himpunan dinyatakan dengan sebuah titik (disebut juga simpul atau vertex), dan tiap pasangan terurut dinyatakan dengan busur (arc)
•    Jika (a, b)  R, maka sebuah busur dibuat dari simpul a ke simpul b. Simpul a disebut simpul asal (initial vertex) dan simpul b disebut simpul tujuan (terminal vertex). 
•    Pasangan terurut (a, a) dinyatakan dengan busur dari simpul a ke simpul a sendiri. Busur semacam itu disebut gelang atau kalang (loop).




Sifat-sifat Relasi Biner
•    Relasi biner yang didefinisikan pada sebuah himpunan mempunyai beberapa sifat.
1.  Refleksif (reflexive)
•    Relasi R pada himpunan A disebut refleksif jika (a, a)  R untuk setiap a  A.
•    Relasi R pada himpunan A tidak refleksif jika ada a  A sedemikian  sehingga (a, a)  R
 
Contoh. 
Tiga buah relasi di bawah ini menyatakan relasi pada himpunan bilangan bulat positif N.
 R : x lebih besar dari y,     S : x + y = 5,    T : 3x + y = 10
Tidak satupun dari ketiga relasi di atas yang refleksif karena, misalkan (2, 2) bukan anggota R, S, maupun T.
•    Relasi yang bersifat refleksif mempunyai matriks yang elemen diagonal utamanya semua bernilai 1, atau mii = 1, untuk i = 1, 2, …, n,

•    Graf berarah dari relasi yang bersifat refleksif dicirikan adanya gelang pada setiap simpulnya.
•    Graf berarah dari relasi yang bersifat refleksif dicirikan adanya gelang pada setiap simpulnya.

2.    Menghantar (transitive)
 •    Relasi R pada himpunan A disebut menghantar jika (a, b)  R dan (b, c)  R, maka (a, c)     R, untuk a, b, c  A.
(a).      R = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3) } bersifat menghantar. Lihat tabel berikut: 
 

(b).   R = {(1, 1), (2, 3), (2, 4), (4, 2) } tidak manghantar karena
(c).   (2, 4) dan (4, 2)  R, tetapi (2, 2)  R, begitu juga (4, 2) dan (2, 3)  R, tetapi (4, 3)  R.   
(d).   Relasi R = {(1, 1), (2, 2), (3, 3), (4, 4) } jelas menghantar
(e).  Relasi R = {(1, 2), (3, 4)} menghantar karena tidak ada (a, b) R dan (b, c)  R sedemikian sehingga (a, c) R.
(f).   Relasi yang hanya berisi satu elemen seperti R = {(4, 5)} selalu menghantar.                                            
Contoh 12. Relasi “habis membagi” pada himpunan bilangan bulat positif bersifat menghantar. Misalkan bahwa a habis membagi b dan b habis membagi c. Maka terdapat bilangan positif m dan n sedemikian sehingga b = ma dan c = nb. Di sini  c = nma, sehingga a habis membagi c.  Jadi, relasi “habis membagi” bersifat menghantar.                                                

Contoh 13. Tiga buah relasi di bawah ini menyatakan relasi pada himpunan bilangan bulat positif N.
    R : x lebih besar dari y,     S : x + y = 6,    T : 3x + y = 10
-  R adalah relasi menghantar karena jika x > y dan y > z maka x > z.
- S tidak menghantar karena, misalkan (4, 2) dan (2, 4) adalah anggota S tetapi (4, 4)  S.
- T = {(1, 7), (2, 4), (3, 1)} menghantar.                  

•    Relasi yang bersifat menghantar tidak mempunyai ciri khusus pada matriks representasinya
•    Sifat menghantar pada graf berarah ditunjukkan oleh: jika ada busur  dari a ke b dan dari b ke c, maka juga terdapat busur berarah dari a ke c.  
Relasi Inversi

• Misalkan R adalah relasi dari himpunan A ke himpunan B. Invers dari relasi R, dilambangkan dengan R–1, adalah relasi dari B ke A yang didefinisikan oleh

   R–1 = {(b, a) | (a, b) e R }

Contoh 17. Misalkan P = {2, 3, 4} dan Q = {2, 4, 8, 9, 15}. Jika kita definisikan relasi R dari P ke Q dengan (p, q) e R  jika p habis membagi q maka kita peroleh

    R  = {(2, 2), (2, 4), (4, 4), (2, 8), (4, 8), (3, 9), (3, 15) }

R–1 adalah invers dari relasi R, yaitu relasi dari Q ke P  dengan

(q, p) e R–1  jika q adalah kelipatan dari p

maka kita peroleh

    R–1  = {(2, 2), (4, 2), (4, 4), (8, 2), (8, 4), (9, 3), (15, 3) }                           

Jika M adalah matriks yang merepresentasikan relasi R
 
maka matriks yang merepresentasikan relasi R–1, misalkan N, diperoleh dengan melakukan transpose terhadap matriks M,

Demikian artikel singkat tentang Matematika Driskrit Bab Relasi, semoga bermanfaat.




Diposting oleh di Tidak ada komentar:

Rabu, 29 Mei 2013

BILANGAN RILL DAN BILANGAN BULAT

# BILANGAN RILL
Dalam matematika, bilangan riil atau bilangan real menyatakan bilangan yang bisa dituliskan dalam bentuk desimal, seperti 2,4871773339… atau 3.25678. Bilangan real meliputi bilangan rasional, seperti 42 dan −23/129, dan bilangan irasional, seperti Ï€ dan . Bilangan rasional direpresentasikan dalam bentuk desimal berakhir, sedangkan bilangan irasional memiliki representasi desimal tidak berakhir namun berulang. Bilangan riil juga dapat direpresentasikan sebagai salah satu titik dalam garis bilangan.[1]
Definisi popular dari bilangan real meliputi klas ekivalen dari deret Cauchyrasional, irisan Dedekind, dan deret Archimides.
Bilangan riil ini berbeda dengan bilangan kompleks yang termasuk di dalamnya adalah bilangan imajiner.


Bilangan riil dapat digambarkan sebagai titik-titik pada garis bilangan yang panjangnya takhingga

Sifat-sifat
Aksioma medan
Bilangan riil, beserta operasi penjumlahan dan perkalian, memenuhi aksiomaberikut.[1][2]. Misalkan x,y dan z merupakan anggota himpunan bilangan riil R, dan operasi x+y merupakan penjumlahan, serta xy merupakan perkalian. Maka:
  • Aksioma 1 (hukum komutatif): x+y = y+x, dan xy = yx
  • Aksioma 2 (hukum asosiatif): x+(y+z) = (x+y)+z dan x(yz) = (xy)z
  • Aksioma 3 (hukum distributif): x(y+z) = (xy + xz)
  • Aksioma 4: Eksistensi unsur identitas. Terdapat dua bilangan riil berbeda, yang dilambangkan sebagai 0 dan 1, sehingga untuk setiap bilangan riil xkita mendapatkan 0+x=x dan 1.x=x.
  • Aksioma 5: Eksistensi negatif, atau invers terhadap penjumlahan. Untuk setiap bilangan riil x, terdapat bilangan riil y sehingga x+y=0. Kita dapat juga melambangkan y sebagai -x.
  • Aksioma 6: Eksistensi resiprokal, atau invers terhadap perkalian. Untuk setiap bilangan riil x tidak sama dengan 0, terdapat bilangan riil y sehinggaxy=1. Kita dapat melambangkan y sebagai 1/x.
Himpunan yang memenuhi sifat-sifat ini disebut sebagai medan, dan karena itu aksioma di atas dinamakan sebagai aksioma medan.
Aksioma urutan
Kita akan mengasumsikan terdapat himpunan R+, yang disebut sebagai bilangan positif yang merupakan himpunan bagian dari R. Misalkan juga x dan y adalah anggota R+. Himpunan bagian ini memenuhi aksioma urutan berikut ini:[2]
  • Aksioma 7: x+y dan xy merupakan anggota R+
  • Aksioma 8: Untuk setiap x yang tidak sama dengan 0, x anggota R+ atau -xanggota R+, tapi tidak mungkin keduanya sekaligus
  • Aksioma 9: 0 bukan anggota R+.
Aksioma kelengkapan
  • Aksioma 10: Setiap himpunan bilangan riil S yang memiliki batas atas memiliki supremum, yakni ada suatu bilangan riil B sehingga B=sup(S).
# BILANGAN BULAT
Bilangan bulat terdiri dari bilangan cacah (0, 1, 2, …) dan negatifnya (-1, -2, -3, …; -0 adalah sama dengan 0 sehingga tidak lagi dimasukkan secara terpisah). Bilangan bulat dapat dituliskan tanpa komponen desimal atau pecahan.
Himpunan semua bilangan bulat dalam matematika dilambangkan dengan Z (atau ), berasal dari Zahlen (bahasa Jerman untuk “bilangan”).
Himpunan Z tertutup di bawah operasi penambahan dan perkalian. Artinya, jumlah dan hasil kali dua bilangan bulat juga bilangan bulat. Namun berbeda dengan bilangan asli, Z juga tertutup di bawah operasi pengurangan. Hasil pembagian dua bilangan bulat belum tentu bilangan bulat pula, karena itu Z tidak tertutup di bawah pembagian.

Tabel sifat-sifat operasi bilangan bulat
PenambahanPerkalian
closure:a + b   adalah bilangan bulata × b   adalah bilangan bulat
Asosiativitas:a + (b + c)  =  (a + b) + ca × (b × c)  =  (a × b) × c
Komutativitas:a + b  =  b + aa × b  =  b × a
Eksistensi unsur identitas:a + 0  =  aa × 1  =  a
Eksistensi unsur invers:a + (−a)  =  0
Distribusivitas:
a × (b + c)  =  (a × b) + (a × c)
Tidak adapembagi nol:jika a × b = 0, maka a = 0 atau b = 0 (atau keduanya)
Bilangan bulat sebagai tipe data dalam bahasa pemrograman
Dalam Pascal
Bilangan bulat (integer) merupakan salah satu tipe data dasar dalam bahasa pemrograman Pascal. Walaupun memiliki ukuran 2 byte (16 bit),karena integeradalah type data signed maka hanya mampu di-assign nilai antara -215 hingga 215-1 yaitu -32768 sampai 32767. Ini disebabkan karena 1 bit digunakan sebagai penanda positif/negatif. Meskipun memiliki istilah yang sama, tetapi tipe data integer pada bahasa pemrograman Visual Basic .NET dan Borland Delphimemiliki ukuran 4 byte atau 32 bit signed sehingga dapat di-assign nilai antara -2,147,483,648 hingga 2,147,483,647.

Diposting oleh di Tidak ada komentar:

Himpunan dan Diagram venn

Dalam matematika, himpunan adalah segala koleksi benda-benda tertentu yang dianggap sebagai satu kesatuan. Walaupun hal ini merupakan ide yang sederhana, tidak salah jika himpunan merupakan salah satu konsep penting dan mendasar dalam matematika modern, dan karenanya, studi mengenai struktur kemungkinan himpunan dan teori himpunan, sangatlah berguna.
Irisan dari dua himpunan yang dinyatakan dengan diagram Venn
Teori himpunan, yang baru diciptakan pada akhir abad ke-19, sekarang merupakan bagian yang tersebar dalam pendidikan matematika yang mulai diperkenalkan bahkan sejak tingkat sekolah dasar. Teori ini merupakan bahasa untuk menjelaskan matematika modern. Teori himpunan dapat dianggap sebagai dasar yang membangun hampir semua aspek dari matematika dan merupakan sumber dari mana semua matematika diturunkan




Notasi Himpunan [sunting]

Hubungan di antara 8 buah set dengan menggunakan diagram Venn
Biasanya, nama himpunan ditulis menggunakan huruf besar, misalnya S, A, atau B, sementara elemen himpunan ditulis menggunakan huruf kecil (a, c,z). Cara penulisan ini adalah yang umum dipakai, tetapi tidak membatasi bahwa setiap himpunan harus ditulis dengan cara seperti itu. Tabel di bawah ini menunjukkan format penulisan himpunan yang umum dipakai.
NotasiContoh
HimpunanHuruf besarS
Elemen himpunanHuruf kecil (jika merupakan huruf)a
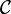
KelasHuruf tulisan tangan\mathcal{C}
Himpunan-himpunan bilangan yang cukup dikenal, seperti bilangan kompleks, riil, bulat, dan sebagainya, menggunakan notasi yang khusus.
BilanganAsliBulatRasionalRiilKompleks
Notasi\mathbb{N}\mathbb{Z}\mathbb{Q}\mathbb{R}\mathbb{C}
Simbol-simbol khusus yang dipakai dalam teori himpunan adalah:
SimbolArti
\{ \} atau \varnothingHimpunan kosong
\cupOperasi gabungan dua himpunan
\capOperasi irisan dua himpunan
\subseteq, \subset, \supseteq, \supsetSubhimpunan, Subhimpunan sejati, Superhimpunan, Superhimpunan sejati
A^CKomplemen
\mathcal{P}(A)Himpunan kuasa
Himpunan dapat didefinisikan dengan dua cara, yaitu:
  • Enumerasi, yaitu mendaftarkan semua anggota himpunan. Jika terlampau banyak tetapi mengikuti pola tertentu, dapat digunakan elipsis (...).
B = \{ apel,\,jeruk,\,mangga,\,pisang\}
A = \{ a,\,b,\,c,\,...,\,y,\,z\}
\mathbb{N} = \{1,\,2,\,3,\,4,\,...\}
  • Pembangun himpunan, tidak dengan mendaftar, tetapi dengan mendeskripsikan sifat-sifat yang harus dipenuhi oleh setiap elemen himpuan tersebut.
O = \{ u\, |\, u \mbox{ adalah bilangan ganjil} \}
E = \{ x\, |\, x \in \mathbb{Z} \and (x \mbox{ mod } 2 = 0)\}
P = \{ p\, |\, p \mbox{ adalah orang yang pernah menjabat sebagai Presiden RI} \}
Notasi pembangun himpunan dapat menimbulkan berbagai paradoks, contohnya adalah himpunan berikut:
A = \{ x\, |\, x \notin A\}
Himpunan A tidak mungkin ada, karena jika A ada, berarti harus mengandung anggota yang bukan merupakan anggotanya. Namun jika bukan anggotanya, lalu bagaimana mungkin A bisa mengandung anggota tersebut.

Himpunan kosong Himpunan {apel, jeruk, mangga, pisang} memiliki anggota-anggota apel, jeruk, mangga, dan pisang. Himpunan lain, semisal {5, 6} memiliki dua anggota, yaitu bilangan 5 dan 6. Kita boleh mendefinisikan sebuah himpunan yang tidak memiliki anggota apa pun. Himpunan ini disebut sebagai himpunan kosong.

Himpunan kosong tidak memiliki anggota apa pun, ditulis sebagai:
\varnothing = \{ \, \}







Diposting oleh di Tidak ada komentar:
Langganan: Postingan (Atom)