PECINTA KEBIJAKSANAAN: Himpunan dan Diagram venn

Rabu, 29 Mei 2013

Himpunan dan Diagram venn

Dalam matematika, himpunan adalah segala koleksi benda-benda tertentu yang dianggap sebagai satu kesatuan. Walaupun hal ini merupakan ide yang sederhana, tidak salah jika himpunan merupakan salah satu konsep penting dan mendasar dalam matematika modern, dan karenanya, studi mengenai struktur kemungkinan himpunan dan teori himpunan, sangatlah berguna.

Irisan dari dua himpunan yang dinyatakan dengan diagram Venn

Teori himpunan, yang baru diciptakan pada akhir abad ke-19, sekarang merupakan bagian yang tersebar dalam pendidikan matematika yang mulai diperkenalkan bahkan sejak tingkat sekolah dasar. Teori ini merupakan bahasa untuk menjelaskan matematika modern. Teori himpunan dapat dianggap sebagai dasar yang membangun hampir semua aspek dari matematika dan merupakan sumber dari mana semua matematika diturunkan

Notasi Himpunan [sunting]

Hubungan di antara 8 buah set dengan menggunakan diagram Venn

Biasanya, nama himpunan ditulis menggunakan huruf besar, misalnya S, A, atau B, sementara elemen himpunan ditulis menggunakan huruf kecil (a, c,z). Cara penulisan ini adalah yang umum dipakai, tetapi tidak membatasi bahwa setiap himpunan harus ditulis dengan cara seperti itu. Tabel di bawah ini menunjukkan format penulisan himpunan yang umum dipakai.

	Notasi	Contoh
Himpunan	Huruf besar	$S$
Elemen himpunan	Huruf kecil (jika merupakan huruf)	$a$
Kelas	Huruf tulisan tangan	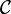$\mathcal{C}$

Himpunan-himpunan bilangan yang cukup dikenal, seperti bilangan kompleks, riil, bulat, dan sebagainya, menggunakan notasi yang khusus.

Bilangan	Asli	Bulat	Rasional	Riil	Kompleks
Notasi	$\mathbb{N}$	$\mathbb{Z}$	$\mathbb{Q}$	$\mathbb{R}$	$\mathbb{C}$

Simbol-simbol khusus yang dipakai dalam teori himpunan adalah:

Simbol	Arti
$\{ \}$ atau $\varnothing$	Himpunan kosong
$\cup$	Operasi gabungan dua himpunan
$\cap$	Operasi irisan dua himpunan
$\subseteq$ , $\subset$ , $\supseteq$ , $\supset$	Subhimpunan, Subhimpunan sejati, Superhimpunan, Superhimpunan sejati
$A^C$	Komplemen
$\mathcal{P}(A)$	Himpunan kuasa

Himpunan dapat didefinisikan dengan dua cara, yaitu:

Enumerasi, yaitu mendaftarkan semua anggota himpunan. Jika terlampau banyak tetapi mengikuti pola tertentu, dapat digunakan elipsis (...).

$B = \{ apel,\,jeruk,\,mangga,\,pisang\}$

$A = \{ a,\,b,\,c,\,...,\,y,\,z\}$

$\mathbb{N} = \{1,\,2,\,3,\,4,\,...\}$

Pembangun himpunan, tidak dengan mendaftar, tetapi dengan mendeskripsikan sifat-sifat yang harus dipenuhi oleh setiap elemen himpuan tersebut.

$O = \{ u\, |\, u \mbox{ adalah bilangan ganjil} \}$

$E = \{ x\, |\, x \in \mathbb{Z} \and (x \mbox{ mod } 2 = 0)\}$

$P = \{ p\, |\, p \mbox{ adalah orang yang pernah menjabat sebagai Presiden RI} \}$

Notasi pembangun himpunan dapat menimbulkan berbagai paradoks, contohnya adalah himpunan berikut:

$A = \{ x\, |\, x \notin A\}$

Himpunan A tidak mungkin ada, karena jika A ada, berarti harus mengandung anggota yang bukan merupakan anggotanya. Namun jika bukan anggotanya, lalu bagaimana mungkin A bisa mengandung anggota tersebut.

Himpunan kosong Himpunan {apel, jeruk, mangga, pisang} memiliki anggota-anggota apel, jeruk, mangga, dan pisang. Himpunan lain, semisal {5, 6} memiliki dua anggota, yaitu bilangan 5 dan 6. Kita boleh mendefinisikan sebuah himpunan yang tidak memiliki anggota apa pun. Himpunan ini disebut sebagai himpunan kosong.

Himpunan kosong tidak memiliki anggota apa pun, ditulis sebagai:

$\varnothing = \{ \, \}$

http://id.wikipedia.org/wiki/Himpunan_(matematika)

PECINTA KEBIJAKSANAAN

Total Tayangan Halaman

Rabu, 29 Mei 2013

Himpunan dan Diagram venn

Notasi Himpunan [sunting]

Tidak ada komentar:

Posting Komentar

Mengenai Saya